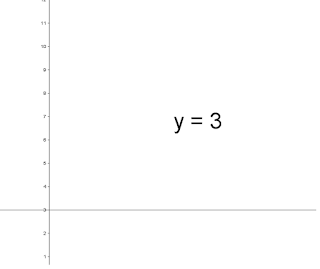TRABAJO DE FUNCIONES

1ª PARTE:CONCEPTOS BÁSICOS 

1.  ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo? 

Mediante una gráfica en la que cada eje sea una magnitud. En el siguiente ejemplo el volumen  se ha colocado en el eje de ordenadas (eje Y), y la masa  se ha colocado en el eje de abscisas (eje X).

2. ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc.

Una función es una correspondencia numérica en la que a cada elemento del conjunto inicial se le asigna un único elemento del conjunto final. Las funciones matemáticas equivalen al proceso lógico común que se expresa como "depende de".

Las relaciones entre magnitudes se pueden expresar mediante:

• Una tabla
• Una gráfica 
• Una ecuación

Las funciones se usan en nuestra vida cotidiana, aquí os dejo unos ejemplos.


Número de transplantes que se han realizado en distintos años

Velocidad de dos trenes

Lo que crece una persona a lo largo de los años

3. ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y  decrecientes? 

Es la relación/división entre "lo que sube y lo que avanza"

• En una función creciente siempre sera un número positivo, ya sea entero o decimal, porque asciende más de lo que avanza. 
• En una función constante siempre dará 0 porque se divide lo que asciende entre lo que avanza (asciende 0 y avanza X, siempre da 0). 
• En una función descendente siempre dará un número negativo ya que el numerador será negativo al descender.

función creciente

función descendente

4. Utilizando la representación gráfica de una o varias funciones, explica la diferencia entre máximos y mínimos absolutos y relativos.

Los máximos y mínimos absolutos se refieren a los puntos que más sobresalen dentro de una función. Los relativos sobresalen pero dentro de una función puede haber varios puntos de este tipo.

5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría.

               

función simétrica respecto al eje y

    

función simétrica respecto al origen

Una función es simétrica respecto al origen si es una función impar, si en la ecuación la x está elevada a un número impar. Una función es impar si cumple: 

                                                                   f (-x) = -f (x)

Una función es simétrica respecto al eje de ordenadas si es una función par, si en la ecuación, la x está elevada a un número par. Una función es par si cumple: 

                                                                   f (-x) = f (x)

6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma.

Se llaman así porque, al igual que los números periódicos, poseen un patrón que se repite.

7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas?

Una función es continua si se pude dibujar en un solo trazo. Y una función es discontinua si su gráfica no se puede dibujar en un solo trazo.

8. Investiga: ¿cuál es el origen del término función?

Una función es el propósito o tarea que se le atribuye a una cosa. Proviene del latín  functĭo, funciōnis, y significa "ejecución, ejercicio de una facultad".

2ª PARTE: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES

Para realizar las actividades propuestas en esta parte puedes utilizar alguno de los programas que te recomiendo: Fooplot, Symbolab, Geogebra, Funciones para Windows, Derive, etc.

9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas. 

a) Función lineal creciente 

b) Función lineal constante 

c) Función lineal decreciente 

d) Rectas paralelas 

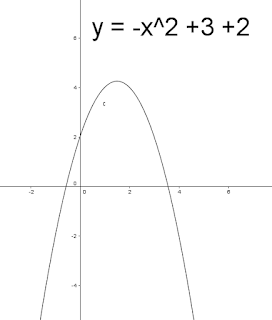
e) Función cuadrática cóncava 

f) Función cuadrática convexa 

Función lineal creciente

 

Función lineal constante
 

Función lineal decreciente

 

Rectas paralelas
 

Función cuadrática cóncava
 

Función cuadrática convexa

 









 12. Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente:

3x -2y = 4

2x +3y = 33

 y = 7 ; x = 6

13. Elige un modelo de coche que disponga de motorizaciones diesel y gasolina y realiza un estudio gráfico de la función coste que nos permita averiguar cual es el automóvil más adecuado para nosotros en función del número de kilómetros que recorremos anualmente. (Nota: Necesitas el precio del coche, el del combustible y el consumo combinado)

 

BMW M3 DKG (gasolina): 90.000 €

BMW 335d (diésel): 54.000 €

Precio de la gasolina: 1,05 €

Precio del diésel: 1,02 €

 



 

14.Interpreta la gráfica del recorrido del Maratón Popular de Madrid

En los primeros 5 km hay una subida hasta los 720 m de altura. A los 10 km baja hasta los 680m de altura. A los 15 km vuelve a bajar hasta los 640m de altura. A los 20 km sube hasta los 670 m de altura. A los 25 km sigue subiendo hasta los 720m de altura. A los 33 km baja hasta los 645 m de altura. A los 36 km sube hasta los 700 m de altura.



MÉTODOS DE SEPARACIÓN DE MEZCLAS

 

1.- OBJETIVOS

• Diferenciar entre mezcla heterogénea y mezcla homogénea.
• Separar los componentes de una mezcla por diferentes procedimientos, en función de las propiedades de sus componentes.
• Experimentar los métodos físicos de separación más comunes.

 

2.- FUNDAMENTO TEÓRICO

La mayoría de las sustancias que encontramos en la naturaleza son mezclas de ellas y se obtienen las sustancias puras mediante diferentes métodos de separación.



Una mezcla es un conjunto de dos o más componentes diferentes que conservan sus propiedades. Existen dos tipos de mezclas: HETEROGÉNEAS y HOMOGÉNEAS.

• Una mezcla HETEROGÉNEA es aquella en la que se pueden distinguir sus componentes.
• Una mezcla HOMOGÉNEA es aquella en la que no se pueden distinguir sus componentes.

Técnicas de separación de sustancias en las mezclas heterogéneas

• Filtración: Separa un sólido insoluble de un líquido.
• Evaporación: Separa sólidos, uno soluble y otro no.
• Decantación: Separa líquidos inmiscibles (que no se mezclan).
• Separación magnética: Separa sólidos magnéticos.
• Sublimación: Separa sólidos volátiles.

Técnicas de separación de sustancias en las mezclas homogéneas

• Cristalización: Separa un soluto de un disolvente, por evaporación y enfriamiento.
• Destilación: Separa dos líquidos inmiscibles, de diferente punto de ebullición.
• Cromatografía: Separa solutos por diferente absorción en un material poroso.

 

3.- DESARROLLO DE LA PRÁCTICA

 

Cristalización

CUESTIONARIO:

-¿Qué tipo de mezcla formaban estas sustancias antes de ser separadas?

 Una mezcla heterogénea
-¿Qué sustancia ha quedado en el filtro?¿cual se ha filtrado?                                    
 No se ha filtrado la arena pero si el agua y sulfato disuelto
-¿De qué color son los cristales?
 Azules.
-¿Cuánto tiempo ha tardado en formarse?
  De un día para otro ya estaba cristalizado.
-¿De qué crees que depende el tamaño de los cristales formados?
   De las cantidades de las sustancias que se echen.

Aquí os dejo una foto de la cristalización

Separación magnética  

 

CUESTIONARIO:

- ¿La mezcla cloruro sódico y limadura de hierro es homogénea o heterogénea?

 Es heterogénea porque se aprecian los componentes.

- ¿Se podría separar el aluminio del azufre con un imán?

 Sí, ya que el aluminio es un metal y se pegaría al imán mientras que el azufre no.

- Cita algún ejemplo en el que se utilice este método de separación.

 Se suele utilizar en química, ya que este método sirve par separar metales de otros elementos que no  lo son
 

 Aquí os dejo algunas de las fotos de la practica:

  

La decantación:

 

CUESTIONARIO:

- ¿Qué tipo de mezcla formaban estas sustancias antes de ser separadas?

   No se mezclaban, eran inmiscibles.

- Identifica la sustancia 1 y la 2.

   La primera sustancia era agua y la segunda aguarrás.

- ¿En qué propiedad de las sustancias se basa esta método de separación?

   La miscibilidad.

- Cita una mezcla formada por otras sustancias diferentes que podrías separar usando esta técnica.

   El agua y el aceite.

 

Aquí os dejo algunas imágenes

 

La cromatografía

 

CUESTIONARIO:

- ¿De qué color era la raya?

    Hicimos puntos de distintos colores: rojo, negro y verde.

- ¿Qué colores han aparecido en el papel de filtro?

    Rojo, azul y morado.

- ¿Cuál es más abundante?

   El rojo.

 

Alguna imagen de la práctica

LA LEYENDA DEL REY SHIRHAM

LA LEYENDA DEL AJEDREZ

Cuenta la leyenda que había en la India un rey llamado Shirham, qué estaba permanentemente aburrido, triste, según se dice por la pérdida de su hijo en el  campo de batalla Así pues, Shirham encargó, a un sabio llamado Lahur, que inventase un juego que le permitiese salir de su tedio.

Transcurrido un tiempo, Lahur presentó al monarca un juego nuevo que se jugaba en un tablero dividido en 64 cuadros (8×8) sobre el cual se situaban fichas de distinto tipo con capacidades de movimiento distintas, intentando simular un campo de batalla. El juego en cuestión era el ajedrez que conocemos hoy en día.

Tan maravillado quedó Shirham por el nuevo juego que le dijo a Lahur que le pidiese lo que quisiera como recompensa de semejante invento. La sorpresa del rey fue mayúscula cuando escucho la petición del sabio, sólo le pedía arroz. Lahur le pidió: un grano de arroz por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta… y así sucesivamente, duplicando en cada casilla la cantidad de la anterior hasta llegar a la última.

El monarca encantado por lo barato que le iba a resultar el juego tan genial, procedió a realizar el pago y……

NO HABÍA ARROZ EN TODO EL REINO PARA PAGAR LA DEUDA.

Por cada casilla, tomamos el doble de granos de arroz que en la anterior, obteniendo una progresión aritmética de primer término 1 y razón 2.

a₁=1, a₂=2, a₃=4, a₄=8, a₅=16, a₆=32 ….

Y la suma de una progresión geométrica de razón r es:

S_n=(a_n*r -a₁)/(r-1)

Siendo n=64, y r=2 se llega a:

S₆₄=(a₆₄*2 -1)/(2-1)=2⁶³*2-1=2⁶⁴-1

Por tanto Lahur había pedido:

18 446 744 073 709 551 615 granos de arroz

GAUSS

LA SUMA DE LOS 100 PRIMEROS NÚMEROS

Cuenta la historia que en el año 1787, cuando Carl Friedrich Gauss tenía apenas 10 años, un alboroto en el aula del colegio provocó que el maestro enojado, pidiera a los alumnos que sumaran todos los números del 1 al 100. Creyendo que el castigo sería tenerlos a todos un buen rato ocupados.

A los pocos minutos, Gauss se levantó del pupitre, y le entregó el resultado de la suma al profesor : 5050. El profesor, asombrado y seguramente creyendo que su alumno había puesto un número arbitrariamente, se dispuso él mismo a hacer la interminable suma. Al cabo de un buen rato, comprobó que, efectivamente, la suma daba como resultado 5050.

Gauss hizo lo siguiente:

Como debía sumar los números del 1 al 100; Es decir:

            1+2+3+4+5+6+……………..+97+98+99+100.

Observó por un momento la secuencia de números y descubrió que si sumaba el primero con el último, el segundo con el anteúltimo y así sucesivamente obtenía siempre el mismo resultado:

(1+100) = (2+99) = (3+98) = …. = (50+51) = 101

Luego, y como entre el número 1 y el 100 tenía 50 pares de números, solo restaba multiplicar por 50 el resultado obtenido.

50 x 101 = 5050.

Mas tarde, Gauss aplicaría el mismo principio para hallar la suma de la serie geométrica y muchas otras series.

Aquí os dejo un video que lo explica:

APROXIMACIONES

Aquí os dejo mi tabla sobre las aproximaciones:

Si quieres descargar la imagen haz clic aquí.

LOS SISTEMAS DE NUMERACIÓN A LO LARGO DE LA HISTORIA

INTRODUCCIÓN:

Los distintos sistemas de numeración utilizaban símbolos distintos, aunque en todos ellos se da el concepto de base: cuando se alcanza un determinado número se hace una marca distinta que los representa a todos ellos. Este número es la base. Se sigue añadiendo unidades hasta que se vuelve a alcanzar por segunda vez el número anterior y se añade otra marca de la segunda clase.

 

SISTEMA DE NUMERACIÓN EGIPCIO:

Los egipcios usaron un sistema de numeración en base 10 usando los jeroglíficos.

Jeroglíficos egipcios

Se podía escribir indistintamente de izquierda a derecha, al revés o de arriba a abajo, cambiando la orientación de las figuras.

 

SISTEMA DE NUMERACIÓN GRIEGO:

Hacia el año 600 a.C se desarrolló el primer sistema de numeración griego. Consistía en un sistema de base decimal en el que se usaban los símbolos tantas veces como fuera necesario.

sistema de numeración griega

La unidad y los números hasta el cuatro se representan usando trazos verticales. Para representar los símbolos de 50, 500 y 5000 se obtienen añadiendo el signo de 10, 100 y 1000 al de 5, usando un principio multiplicativo.

 

SISTEMA DE NUMRACIÓN ROMANO:

Se desarrolló en la antigua Roma y se utilizó en todo el imperio. Como símbolo se usan siete letras mayúsculas a las que se ha asignado un valor numérico. Como regla general se escriben y leen de izquierda a derecha y son ubicados de mayor a menor valor.

sistema de numeración romano

 

SISTEMA DE NUMERACIÓN AZTECA:

En México, entre los siglos XIV y XVI , se desarrolló la civilización azteca. Los aztecas crearon un sistema de cifras que conocemos a partir de manuscritos que los especialistas llaman Codex. En ellos los escribas expresaban por escrito los resultados de sus inventarios y el recuento de los tributos recogidos por el imperio reproduciendo cada cifra tantas veces como fuera necesario junto a los pictogramas asociados.

SISTEMA DE NUMERACIÓN AZTECA

Esta numeración se basa en el principio aditivo según el cual el valor de una representación se obtiene sumando los valores de las cifras. Era una numeración de base vigesimal (20).

 

SISTEMA DE NUMERACIÓN CHINO:

La forma clásica de escritura de los números en China se empezó a usar desde el 1500 AC. aproximadamente. Es un sistema decimal estricto que usa las unidades y las distintas potencias de 10. Utiliza los ideogramas de la figura y usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar para según el principio multiplicativo representar 50, 700 ó 3000.

sistema de numeración chino

VÍDEO

Aquí os dejo un video para ampliar un poco más, trata sobre la sucesión de Fibonacci.